Qualitätssicherung ist eine wichtige Funktion in Unternehmen. Bei der Qualitätssicherung geht es um einen Optimierungsprozess, mit dem regelmäßig erreicht wird, dass das Maß an Qualität erzielt wird, das erforderlich ist, um die von Kunden erwartete Funktionalität zu erfüllen, ohne unnötigen Aufwand darüber hinaus zu betreiben. Die kundenseitige Zahlungsbereitschaft ist die Währung, mit der Qualität aufgewogen wird.
Erwartungen an die Qualitätssicherung
Die Erwartungen an die Qualität werden von den Zielkunden definiert. Deshalb ist eine klare Positionierung im Markt eine wesentliche Voraussetzung für die Vorgaben an das zu erfüllende Qualitätsniveau. Weil die Kriterien für die Qualität unmittelbar von der strategischen Ausrichtung abhängen, muss ein sinnvolles Qualitätsmanagement an die strategische Ausrichtung gekoppelt werden. Ist die strategische Ausrichtung unscharf, wird das Qualitätsmanagement keine optimalen Ergebnisse liefern können.
Um Missverständnissen vorzubeugen: Wenn die Strategie eine Kosten- und Preisführerschaft vorgibt, konzentriert sich gutes Qualitätsmanagement auf das Erreichen der Kosten- und Preisführerschaft. Im Vordergrund für die Qualitätssicherung wird dann stehen, das Qualitätsniveau umzusetzen, das erforderlich ist, damit die Produkte oder Dienstleistungen von Zielkunden gerade akzeptiert werden. Jede Bemühung um einen höheren Qualitätsgrad sollte verworfen werden, wenn dadurch Kosten oder Preise steigen würden. Die Qualitätsziele werden also im Top-Management durch strategische Vorgaben definiert, die sich idealerweise an der Nachfrage und am Wettbewerb orientieren.
Qualitätsmanagement vs. Qualitätssicherung
Das Qualitätsmanagement ist Bestandteil des Top-Managementprozesses. Im Qualitätsmanagement werden die Vorgaben für die System-, Prozess- und Produktqualität definiert. Außerdem dient das Qualitätsmanagement dazu, ein System aus Prozessen zu entwickeln und zu betreiben, das es ermöglicht, die definierte Produktqualität regelmäßig zu erreichen.
Eine wirksame Qualitätssicherung hängt stark von der Güte des Qualitätsmanagements und dessen Eignung, für eine hohe Prozessqualität zu sorgen, ab. Die Empfehlung eines solchen Prozessfokus wurde mit der novellierten Norm DIN-EN-ISO 9001-2015 dokumentiert, nach der sich Organisationen ihre Qualitätsmanagementsysteme zertifizieren lassen können.
Gute Prozesse zeichnen sich dadurch aus, dass sie die Wahrscheinlichkeit für Risiken minimieren und für den Fall, dass doch einmal ein Risiko eintreten würde, die Risikoauswirkungen beherrschbar halten. Eine wesentliche Komponente eines wirksamen Qualitätsmanagements besteht also darin, Bedingungen zu schaffen, die den Eintritt von Risiken möglichst ausschließen. Ein effektives Risikomanagement stützt sich auf statistische Grundlagen, von denen operative Maßnahmen zur Risikoabwendung bzw. -abfederung abgeleitet werden.
Die Qualitätssicherung ist eine operative Funktion im Operations-Management, deren Aufgabe darin liegt, die Vorgaben des Qualitätsmanagements im Rahmen der definierten Prozesse in der betrieblichen Praxis regelmäßig zu erfüllen. In der Qualitätssicherung werden dafür geeignete Methoden ausgewählt und eingesetzt. Die Qualitätssicherung ist quasi in der Rolle der Executive, während das Qualitätsmanagement die Rolle der Legislative einnimmt. Allerdings ist die Qualitätssicherung nicht nur eine dem Qualitätsmanagement nachgelagerte Funktion, sondern als Teil des Qualitätsmanagements zu verstehen. Das Qualitätsmanagement ist also ein Gesamtkonzept zur Optimierung der Qualität, wobei Optimierung nicht mit Maximierung gleichzusetzen ist.
Unzureichende Qualität ist nämlich genauso teuer wie überzogene Qualität. Um Kundenunzufriedenheit einerseits und nicht wertgeschätzten Blindaufwand andererseits zu vermeiden, müssen sich sowohl das Qualitätsmanagement als auch die Qualitätssicherung durch den gesamten Geschäftsprozess ziehen. Nicht nur Nacharbeit und Ausschuss, sondern auch Kundenreklamationen und Kundenverluste kosten oft mehr als geeignete Maßnahmen, die eine kommerziell akzeptierte Qualität sichern. Der Kostendruck zwingt im Grunde zu einem funktionierenden Qualitätsmanagement und einer funktionierenden Qualitätssicherung.
Methoden der Qualitätssicherung
Präventive und reparative Maßnahmen: Optimierung der Qualitätskosten
Das Qualitätsmanagement gibt Maßnahmen vor, mit denen das definierte Qualitätsniveau regelmäßig erreicht werden sollen. Die Maßnahmen werden strikt in Vorbeugemaßnahmen (präventive Maßnahmen) und Korrekturmaßnahmen (reparative Maßnahmen) unterschieden.
In Organisationen, in denen kein integriertes Qualitätsmanagement im Einsatz ist, werden die reparativen Maßnahmen überwiegen. Dementsprechend werden sich die Ressourcen auf die Behebung eingetretener Fehler und die Schadensbegrenzung konzentrieren. Aktivitäten wie die Qualitätsüberprüfung nach erfolgten Arbeitsschritten, das Aussortieren fehlerhafter Ware, das Nacharbeiten fehlerhafter Artikel, der Umgang mit Ausschuss, das Bearbeiten kundenseitiger Reklamationen und die Kundenrückgewinnung stehen im Vordergrund bei solchen Unternehmen. Das sind vom Charakter her Aktivitäten der Qualitätssicherung.
In Organisationen, die ein integriertes Qualitätsmanagement im Einsatz haben, werden vorbeugende Maßnahmen zur Qualitätssicherung ergriffen. Dazu zählen die Definition robuster Prozesse und das Führen der Qualität über die Güte der Prozesse. Die Philosophie besteht darin, dass die Produktqualität den Anforderungen entspricht, wenn eine hinreichende Prozessgüte definiert ist und die Prozesse zuverlässig befolgt werden. Es werden also nicht mehr die Eigenschaften jedes Artikels überprüft, sondern vielmehr die Prozessparameter. Dafür müssen die Prozesse durch eine geeignete Regelung innerhalb eines „grünen Bereichs“ gehalten werden, der statistisch eine kommerziell akzeptable Produktqualität sicherstellt. Um dahin zu gelangen ist Schulung erforderlich. Die Regelung von Prozessen und die Personalschulung sind ebenfalls präventive Qualitätsmaßnahmen.
Je umfassender und wirksamer die präventiven Maßnahmen gewählt werden, desto geringer fallen die reparativen Maßnahmen aus. Leider ist die Maximierung der präventiven Maßnahmen aber nicht der Königsweg. Denn die Qualitätskosten sind als die Summe der Kosten aus präventiven und reparativen Maßnahmen definiert. Also muss der Mix aus präventiven und reparativen Maßnahmen so optimiert werden, dass die Qualitätsanforderungen zu den minimal möglichen Kosten erfüllt werden. Diese Optimierungsaufgabe ist eine laufende Herausforderung im Qualitätsmanagement.
Kontinuierlicher Verbesserungsprozess (KVP)
Wozu nützt ein kontinuierlicher Verbesserungsprozess?
Eng mit der Qualitätssicherung verbunden ist die Methode des kontinuierlichen Verbesserungsprozesses. Die Idee dahinter ist, über die bestehende Arbeitsweise immer wieder kritisch zu reflektieren und nach weiteren Verbesserungsmöglichkeiten zu suchen. So ergibt sich aus einer Reihe von kleinen Verbesserungsschritten ein immer höheres Maß an Qualität bzw. sinkende Qualitätskosten. Die Herausforderung bei der kontinuierlichen Verbesserung besteht darin, das richtige Maß zu finden. Es ist keine Selbstverständlichkeit, einen kontinuierlichen Verbesserungsprozess überhaupt einzuführen und lebendig zu halten. Andererseits sollte das Qualitätsniveau nicht über das Maß hinaus gesteigert werden, für das Kunden eine Zahlungsbereitschaft aufweisen. Vor allem geht es darum, sicherzustellen, dass die definierte Qualität mit hoher Wahrscheinlichkeit erreicht wird. Oft geht es bei dem kontinuierlichen Verbesserungsprozess auch darum, die kommerziell vernünftige Qualität zu immer geringeren Kosten zu erbringen.
Im Zusammenhang mit der Qualitätssicherung geht es bei der kontinuierlichen Verbesserung darum, die eingesetzten Methoden und Mittel weiterzuentwickeln, mit der die Produktqualität gesichert werden soll. Die Ziele der kontinuierlichen Verbesserung bestehen darin, mit weniger Aufwand sicherzustellen, dass die definierte Produktqualität zuverlässig erreicht bzw. dass die Produktqualität auf eine modifizierte Weise erreicht wird. Die kontinuierliche Verbesserung kann sich also sowohl auf die Produkterstellung selbst als auch auf die Art und Weise der Überprüfung der Produktqualität beziehen.
Wie kann ein kontinuierlicher Verbesserungsprozess in Unternehmen eingeführt werden?
Ein kontinuierlicher Verbesserungsprozess lässt sich in die Qualitätssicherung einführen, indem Mitarbeiter in der Qualitätssicherung und in den operativen betrieblichen Funktionen darauf geschult werden, ihre Arbeit ständig kritisch zu hinterfragen und inkrementell weiterentwickeln. Führungskräfte sollten das eigene Engagement der Mitarbeiter für laufende Verbesserungen einfordern und wertschätzen, indem sie dafür sorgen, dass die eingebrachten Ideen zur laufenden Verbesserung transparent geprüft, beurteilt und bei Eignung in die Umsetzung gebracht werden.
Innovationsprozess: Wenn Bestehendes nicht mehr weiterführt
Wozu nützt ein Innovationsprozess?
Der Innovationsprozess ist ein weiteres Element der Qualitätssicherung. Allerdings ist der Innovationsprozess ganz anders gelagert als der kontinuierliche Verbesserungsprozess. Beim Innovationsprozess geht es darum, die Voraussetzungen zu schaffen, um über das Bestehende, das Vertraute, die Routine hinaus ganz neue Ansätze zu entwickeln, die definierte Qualität zu erreichen bzw. den erreichten Qualitätsgrad zu verifizieren.
Innovation beinhaltet also ganz neue Methoden der Qualitätssicherung bzw. ganz andere Verfahren und/oder Materialien der Produkterstellung. Innovation beginnt bei der kreativen Ideenentwicklung und setzt sich über die konzeptionelle Ausarbeitung fort bis zur erfolgreichen Einführung einer Neuerung.
Wie kann ein Innovationsprozess in die Qualitätssicherung eingeführt werden?
Üblicherweise werden eingeführte Verfahren, Methoden und Pfade erst verlassen, wenn sie keine gewünschten Resultate mehr liefern. Oft wird erst dann ein kreativer Prozess in Gang gesetzt, um neue Wege zu finden. Wir leben in einer schnelllebigen (Wirtschafts-) Welt, in der die Zyklen kürzer werden. Deshalb kommen eingeschlagene Wege früher an ihre Grenzen als das früher der Fall war. Insofern liegt die Frage nahe, ob immer erst ein Engpass vorliegen muss, um neue Wege zu suchen, oder ob nicht ein Innovationsprozess für die Qualitätssicherung eingeführt werden kann, über den laufend nach ganz neuen Ansätzen gesucht wird.
Der Qualitätszirkel
Edward Deming führte bereits in den 1980er Jahren in die Unternehmensführung den Qualitätszirkel ein, der inzwischen aus fünf Schritten besteht und eine Grundlage für normkonformes Qualitätsmanagement bildet:
Zielsetzung
Der erste Schritt auf dem Weg zum Erreichen von Ergebnissen besteht im Festlegen von Zielsetzungen. Die Zielsetzungen sollten möglichst konkret gefasst werden, so dass deren Erreichungsgrad messbar ist. Für sinnvolle Zielsetzungen hat sich das SMART-Prinzip bewährt:
Ziele sollen
- spezifisch,
- messbar,
- anspruchsvoll und
- realistisch sein
- sowie mit einer Frist versehen werden.
- Messen
Die erreichten Ergebnisse müssen nicht nur messbar sein, sondern auch gemessen werden. Nur was gemessen wird, kann auch beurteilt werden.
Analysieren
Im nächsten Schritt müssen die gemessenen Ergebnisse mit den gesetzten Zielen verglichen und Abweichungen analysiert werden. Um die Ursachen für die Abweichungen zu ermitteln, empfiehlt sich die Methode der Root-Cause-Analyse.
Justieren (act)
Dann geht es darum, die erkannten Ursachen für die Abweichungen zu eliminieren, indem geeignete Maßnahmen eingeleitet werden.
Auswerten (evaluate)
Schließlich muss ausgewertet werden, ob die Maßnahmen tatsächlich greifen und sich in verbesserten Ergebnissen niederschlagen. Andernfalls können entweder bessere Maßnahmen ergriffen werden oder die Ziele angepasst werden.
Erfassung von Qualitätskennzahlen
Qualitätskennzahlen sind Werte, die sich aus der Ausprägung bestimmter Merkmale (Variablen) für Merkmalsträger ergeben. Merkmale können in drei Kategorien unterschieden werden, die verschiedene sinnvolle Auswertungsmöglichkeiten nahelegen.
- Die Ausprägung quantitativer Merkmale kann eindeutig gemessen werden. Jede beliebige Zahl innerhalb eines vernünftigen Rahmens kommt als Messwert infrage. Solche Variablen sind deshalb in der Regel kontinuierlich bzw. stetig. Quantitative Merkmale eignen sich für die Ermittlung der Standardabweichung, die ein Maß für die Variabilität der Merkmalsausprägungen ist.
- Ordinale Merkmale sind Merkmale, deren Ausprägung auf einer Skala eingeordnet werden kann. Das können bspw. Beurteilungen oder Ratings sein. Solche Skalen zwingen in der Regel zu einer Zuordnung zu einer Stufe. Die Variablen sind dadurch diskontinuierlich bzw. diskret.
- Qualitative Merkmale sind diskrete Zustände wie „Farbe Rot“, „Aggregatszustand Flüssig“, „Ausschuss“ oder „Gutware“ etc. Ein Durchschnittswert bei solchen Merkmalen nicht sinnvoll.
Messwerte von Merkmalen schwanken bzw. streuen durch systematische Abweichungen, zufällige Abweichungen oder Messfehler. Ursachen solcher Abweichungen können die 5 „M“ der Mensch (Prozessführung), die Maschine (Schwingungen, Verschleiß etc.), die Methode, das Material (z. B. die chemische Zusammensetzung) und das Milieu (Wärme, Kälte, Staub etc.).
Es gibt verschiedene Möglichkeiten, die Ausprägung solcher Merkmale zu erfassen. Manche Kennzahlen können 1:1 Messungen oder Zählungen entnommen werden. Andere können nur statistisch ermittelt werden. Um die Auswertung zu vereinfachen, können die Messungen gerundet und zu Messwertklassen oder Kategorien zusammengefasst werden.
Bei großen Grundgesamtmengen werden in der Regel statistische Verfahren angewandt. Unterschieden wird zwischen deskriptiver und induktiver Statistik.
- Deskriptive Statistik wird dazu eingesetzt, Merkmale vorhandener Daten zu beschreiben, indem Regeln erkannt und die Daten nach diesen Regeln ausgewertet werden, beispielsweise Gleichheit, Summen, Durchschnittswerte, Rangordnungen oder zeitliche Entwicklungen zu erkennen.
- Induktive Statistik ist nützlich, um aus repräsentativen Stichprobendaten auf Gesamtdaten zu schließen. Das kann sinnvoll sein, wenn es zu aufwändig wäre, die Ausprägung der Merkmale (Variablen) der Grundgesamtheit zu erfassen.
Im Zuge der Auswertung einer Stichprobe wird zunächst die absolute Häufigkeit der relevanten Merkmalsausprägungen festgestellt. Die Verteilung der Messwerte einer Variablen ergibt die Häufigkeitsverteilung. Nun kann man die Werte jeder Merkmalsausprägung auf die Stichprobenumfang beziehen und erhält die relative Häufigkeitsverteilung, die üblicherweise in Prozent angegeben wird.
Statistische Kennzahlen für das Qualitätsmanagement
Der Modalwert (Mod) ist der Wert einer Messreihe, der am häufigsten vorkommt. Wenn zwei oder mehr Werte häufig vorkommen, haben wir es mit einer bimodalen bzw. einer polymodalen Verteilung zu tun.
Der Median (Md) ist der Wert einer Messreihe, der die nach Größe sortierten Werte in zwei genau gleich große Hälften teilt.
Die Percentile bzw. Quartile zeigt den Wert an, der von p Prozent der Merkmalsträger nicht über- oder unterschritten wird.
Das arithmetische Mittel ist der Quotient aus der Summe aller Messwerte und der Anzahl der Messwerte. Es ist der Mittelwert aller Messwerte.
Bei Wachstumsentwicklungen empfiehlt sich das geometrische Mittel, das die n-te Wurzel aus dem Quotienten des Endwertes und des Anfangswertes ist. N ist die Anzahl der Perioden, die betrachtet werden.
Verteilungen von Messwerten müssen nicht symmetrisch sein. Eine unimodale, symmetrische Verteilung ist die Gauß’sche Normalverteilung. Es kann aber auch eine rechtsschiefe oder eine linksschiefe Verteilung vorliegen.
Die Verteilung der Ausprägungen um den Mittelpunkt ist die Streuung der Messwerte. Bei gleichem arithmetischem Mittelwert kann die Streuung sehr unterschiedlich sein. Das Maß für die Streuung ist die durchschnittliche Abweichung der Messwerte vom arithmetischen Mittel (average deviation AD). Je geringer die Streuung, desto stabiler ist der Prozess. In der Praxis möchte man besonders große Abweichungen vom Mittelwert besonders stark gewichten. Das kann dadurch berücksichtigt werden, dass die Quadrate der Abweichungen in die Berechnung Streuung einfließen. Die so ermittelte Streuung bezeichnet man als Varianz σ2. Die Wurzel aus der Varianz ist die Standardabweichung σ. Sie beziffert die Häufigkeitsverteilung der Messwerte einer Messreihe um einen Mittelwert. Die Standardabweichung ist bei unimodalen, annähernd symmetrischen Verteilungen aussagekräftig.
Bei einer Gauß’schen Normalverteilung liegen im Bereich zwischen dem Skalenwert x – σ und dem Skalenwert x + σ genau 2/3 aller Merkmalsträger und im Bereich zwischen dem Skalenwert x – 2σ und dem Skalenwert x + 2σ genau 95 % aller Merkmalsträger.
Relevant ist auch der Range, also die Variationsbreite zwischen dem kleinsten und dem größten Messwert. Damit Ausreißer die Aussage nicht verfälschen, ist es sinnvoll, die untersten und die obersten 5 %, also der ersten 5 und der letzten 5 Percentile, aus der Betrachtung herauszunehmen.
Wahrscheinlichkeitsrechnung für das Qualitätsmanagement
Bei künftigen Vorgängen, die gewissen Schwankungen unterworfen sind, wie die Dauer von Rüstzeiten, die Reparaturdauer, der Ausschussanteil etc., kann die Wahrscheinlichkeitsrechnung helfen, trotz der Unsicherheit zu vernünftigen Annahmen zu gelangen. Dahinter steckt die Erkenntnis, dass sich der durchschnittliche Wert hinreichend vieler bekannter Vorgänge dem wahrscheinlichen Wert für künftige Vorgänge annähert. Wichtig ist es zu berücksichtigen, dass eine bestimmte Vorgeschichte keinerlei Einfluss auf die Zukunft hat. Laut Joseph Bertrand, französischer Mathematiker, hat die Statistik „weder Gewissen noch Gedächtnis“.
Der Wahrscheinlichkeitsbegriff von Laplace gibt das Verhältnis der günstigen Fälle zu der Anzahl aller Fälle an. Die Wahrscheinlichkeit zusammengesetzter Ereignisse (Wie wahrscheinlich ist es, mit zwei Würfeln eine „4“ oder in der Summe eine Augenzahl von „6“ zu würfeln?) lässt sich rechnerisch mit dem Additionssatz ermitteln. Die Wahrscheinlichkeit gekoppelter Ereignisse (Wie wahrscheinlich ist es, erst „1“ und dann „6“ zu würfeln?) lässt sich mit dem Multiplikationssatz errechnen. (Wie wahrscheinlich ist es, in drei Würfen mindestens einmal eine „6“ zu würfeln?): P = 1 – (½ x ½ x ½) = 7/8.
Interessant kann auch sein, die Wahrscheinlichkeit eines Ereignisses auszurechen, wenn nur unvollständige Informationen vorliegen. (Sie möchten eine „1“ würfeln, wissen von Ihrem Wurf aber nur, dass es sich um eine ungerade Zahl handelt. Dann beträgt die Wahrscheinlichkeit, dass Sie eine „1“ gewürfelt haben: P = 1/3.
Auch die Kombinatorik kann nützlich sein, um die Wahrscheinlichkeit von Ereignissen zu berechnen. Besonders praktisch sind Permutationen (mit und ohne Wiederholung).
Kennzahlen für die Qualitätssicherung
Wofür werden in der Qualitätssicherung Kennzahlen gebraucht?
Produktionsprozesse sind komplex. Die Anlagenverfügbarkeit, die Produktionsleistung, die Produktionskosten und die Produktionsqualität werden von vielen angrenzenden Funktionen beeinflusst, die miteinander und mit der Produktion in Wechselwirkung stehen. Entsprechend vielschichtig muss die Beurteilung der Produktionsleistung ausfallen. Eine einzelne Leistungszahl kann einen Gesamtüberblick geben, ist aber nicht dazu geeignet, die tatsächlichen Verhältnisse in der Produktion gezielt zu erfassen und sie optimieren. Für eine operative Führung und eine Verbesserung der Produktionseckdaten sind weitere Kennzahlen erforderlich.
Sinnvoll sind nicht nur einfache Messwerte in der Produktion, sondern Kennzahlen, die verschiedene Messwerte miteinander oder Messwerte mit Zielvorgaben ins Verhältnis setzt. Dadurch können Abhängigkeiten dargestellt werden.
Außerdem empfehlen sich Zeitreihen von Kennzahlen, um Tendenzen zu erkennen und Entwicklungen zu führen.
Welche Kennzahlen sind für die Qualitätssicherung sinnvoll?
Um die Leistungsfähigkeit und Wirksamkeit der Qualitätssicherung zu erfassen und gezielt zu entwickeln, bieten sich QS-Kennzahlen als Grundlage an. Mit der zeitlichen Entwicklung kann festgestellt werden, ob Maßnahmen wirklich greifen und wo Verbesserungspotenzial besteht. Es können auch Tendenzen erkannt werden. Diese Information kann dazu eingesetzt werden, steuernd einzugreifen. Dadurch können interne Prozesse stabilisiert, Kosten gesenkt und Kundenanforderungen regelmäßiger erfüllt werden.
QS-Kennzahlen lassen sich entlang des gesamten Geschäftsprozesses anlegen und erfassen. Das ist kein Thema einer Abteilung „Qualitätssicherung“, sondern ein übergreifendes General Management-Thema. Insofern sollte das Management sicherstellen, dass alle Prozesse, die im Unternehmen ausgeführt werden, Kennzahlen liefern. Erfasst werden diese Kennzahlen in den betrieblichen Funktionen, also in der Produktion, in der Logistik, im Vertrieb, in der Verwaltung etc. Wertvoll werden diese QM-Kennzahlen allerdings erst in ihrer Verknüpfung. Erst daraus lassen sich Maßnahmen für eine ganzheitliche Optimierung ableiten. Die Erkenntnis, dass die ganzheitliche Optimierung in der Regel ein Kompromiss ist, ist besonders wichtig. Würde nämlich versucht, jede Kennzahl für sich zu optimieren, führte dies zu Interessenkonflikten, Reibung und Kollisionen. Bei der Betrachtung einzelner Kennzahlen ist deshalb immer auf deren Beitrag zum Gesamtergebnis zu achten.
Die QM-Kosten besteht in der Summe der präventiven und der reparativen QM-Kosten. Deshalb ist die separate Erfassung aller präventiver und aller reparativer Qualitätsaufwendungen interessant. Die Analyse kann zu einer Optimierung der Gesamtkosten führen, indem entweder das Engagement in präventive Maßnahmen erhöht oder zurückgefahren wird. Zu den präventiven Maßnahmen zählen Initiativen zur Prozessverbesserung, Standardisierung, Schulungen und Audits. Zu den reparativen Maßnahmen zählen Ausschuss, Nacharbeitskosten, Kapazitätsverlust, und Kosten für jede Überspezifikation, aber auch Reputations- und Kundenverluste sowie der damit verbundene Wiedergewinnungsaufwand.
Die Verfügbarkeit wird auch durch die Zuverlässigkeit der Maschinen- und Anlagen beeinflusst. Eine gängige Kennzahl für die Zuverlässigkeit ist die Mean Time to Repair (MTTR).
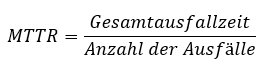
Eine weitere für die Produktion nützliche Kennzahl ist die Mean Time between Failure (MTBF), aus der die Zuverlässigkeit von Maschinen und Anlagen hervorgeht. Die MTBF gibt die Zeit an, in der die Maschine oder Anlage durchschnittlich störungsfrei funktioniert. Sie ist damit ein Maß für das Prozessrisiko.
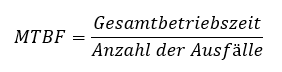
Produktionsausfälle: Wie können Produktionsausfälle sinnvoll gemessen werden?
Produktionsausfälle können aufgelistet werden. Moderne CNC-Maschinen, die mit einem Betriebsdatenerfassungssystem verknüpft sind, können Produktionsausfälle mit ihren Zeiten automatisch erfassen. Den Ausfallzeiten können Gründe zugewiesen werden. Auf grober Ebene unterscheidet man zwischen organisatorischen und technischen Gründen. Zu den organisatorischen Gründen zählen beispielsweise Materialmangel, Personalmangel und kurzfristig erforderliche zusätzliche Rüstvorgänge. Zu den technischen Gründen zählen Anlagenfehler, ungeeignetes Vormaterial, Werkzeugbruch und erkannte Qualitätsmängel.
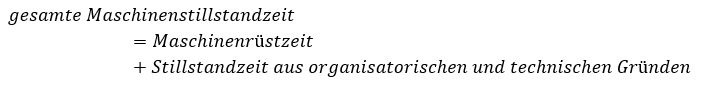
Abgeleitet von der MTBF wird auch die Probability Failure per Hour (PFH) als Kennzahl eingesetzt, die die durchschnittliche Wahrscheinlichkeit eines Ausfalls pro Stunde wiedergibt.
Im Maschinen- und Anlagenbau, wo kleinere Losgrößen produziert werden, wird häufig das „Performance Level“ in Anlehnung an EN ISO 13849-1 eingesetzt.
In der Prozessindustrie und in produzierenden Unternehmen mit großen Losgrößen (Massenfertigung) wird gern das „Safety Integrity Level“ nach IEC 62061 eingesetzt, das ursprünglich für elektrische, elektronische Systeme und für programmierbare Systeme entwickelt wurde.
Produktionsausschuss: Wie kann der Produktionsausschuss überwacht und beurteilt werden?
Der Produktionsausschuss ist eine weitere wichtige Produktionskennzahl. Gemessen wird der Produktionsausschuss als Quotient aus der Ausschussmenge dividiert durch die Gesamtproduktionsmenge.
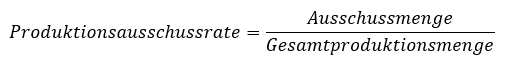
Gerade bei der Ausschusskennzahl muss man darauf achten, worauf sich der Ausschuss bezieht: auf die Gesamtproduktionsmenge oder auf die Gutmenge. Bei geringen Ausschussraten ist diese Unterscheidung irrelevant. Wenn allerdings 50 % der produzierten Menge Ausschuss sind, dann beträgt der Ausschuss, bezogen auf die Gutmenge 100 %. Dieses Extrembeispiel veranschaulicht, wie es zu Missverständnissen kommen kann, wenn die Bezugsgröße nicht eindeutig definiert wird.
Ausschuss verbraucht Material, verursacht Personalkosten und durchläuft Produktionsmaschinen, nimmt also Kapazität und Energie in Anspruch.
Liefertreue: Wie viele Aufträge werden vollständig und termingerecht geliefert?
Die Liefertreue wird maßgeblich, aber nicht ausschließlich von der Produktion beeinflusst. Sie ist definiert durch den Anteil an Aufträgen, die in richtiger Ausführung vollständig und termingerecht ausgeliefert werden, an der Anzahl der Gesamtaufträge. Die Liefertreue wird durch die Supply-Chain-Management-Kennzahl OTIF (on-time in full) definiert.
Um OTIF zu ermitteln, muss die Anzahl der Aufträge erfasst werden, die zum vereinbarten Termin aus- bzw. angeliefert worden sind (OT), und die Anzahl der Aufträge, die vollständig ausgeliefert worden sind (IF).
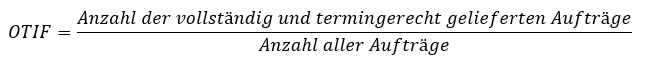
Instandhaltungskosten: Wie können die Instandhaltungskosten überwacht werden?
Wartungs- und Instandhaltungskosten nehmen mit zunehmendem Maschinenalter zu. Gleichzeitig nehmen die Finanzierungskosten ab, wenn Maschinen weitgehend bezahlt sind. Insofern konkurrieren Wartungs- und Instandhaltungskosten mit Investitionen für neue Maschinen oder Anlagen.
Argumente gegen alte Maschinen können die sinkende Zuverlässigkeit und die abnehmende Verfügbarkeit sein. Mit steigendem Ausfallrisiko nimmt die Prozessqualität in der gesamten Produktion und im gesamten Unternehmen ab. Daraus entstehende Produktionsrückstände können sehr hohe Kosten verursachen. Bei Maschinen, die nur gelegentlich eingesetzt werden, mag diese Betrachtung unkritisch sein, aber bei Maschinen, die maßgeblich den Produktionsprozess beeinflussen, empfiehlt sich eine Analyse als Entscheidungsgrundlage.
Insofern empfiehlt sich eine Abwägung der Gesamtkosten für Bestandsmaschinen mit den Gesamtkosten für neue Maschinen.
Ideale Stichprobengröße
Eine typische Frage in der Qualitätssicherung ist, wie groß eine Stichprobe sein muss, um eine valide Aussage darüber zu treffen, wie wahrscheinlich der Eintritt eines Ereignisses in der Gesamtmenge ist. Die Beantwortung dieser Frage ist überhaupt nicht trivial.
Worum geht es hier? Sowohl die Entnahme als auch die Auswertung von Stichproben sind teuer. Aber je kleiner die Stichprobe gewählt wird, desto höher ist die Wahrscheinlichkeit, dass die aus der Stichprobe gewonnene Aussage nicht repräsentativ und damit fehlerhaft ist. Je größer die Stichprobe, desto näher wird das gewonnene Ergebnis am Wert für die Gesamtmenge liegen. Die Abweichung zwischen dem wahrscheinlichen Stichprobenergebnis und der Realität wird als Konfidenzintervall bezeichnet. Das Ergebnis wird als das Stichprobenergebnis +/- das Konfidenzintervall angegeben. Das bedeutet, dass ein Ereignis mit einer bestimmten Wahrscheinlichkeit eintreten wird, aber eine Streuung dieser Wahrscheinlichkeit in der Größenordnung des Konfidenzintervalls berücksichtigt werden muss. Das Konfidenzniveau (in Prozent) gibt an, wie wahrscheinlich es ist, dass das tatsächliche Ergebnis innerhalb einer gewissen Toleranz um das Stichprobenergebnis herum liegen wird. Je höher das Konfidenzniveau, desto präziser lässt die Stichprobe auf die untersuchten Ereignisse in der Gesamtmenge schließen.
Die benötigte Stichprobengröße lässt sich mittels der Standardabweichung σ ermitteln. In der Regel wird eine Standardabweichung σ = 0,5 angesetzt, um zu einer aussagekräftigen Stichprobengröße zu gelangen. Aus dem Konfidenzniveau wird ein Z-Wert ermittelt, der den Abstand zwischen dem Wert und dem tatsächlichen Wert der Gesamtmenge repräsentiert. Der Z-Wert kann statistischen Tabellen entnommen werden. Beispielhaft werden die Z-Werte in Abhängigkeit ausgewählter Konfidenzniveaus gezeigt:
| Konfidenzniveau | Z-Wert |
| 0,80 | 1,28 |
| 0,85 | 1,44 |
| 0,90 | 1,65 |
| 0,95 | 1,95 |
Die Mindestgröße einer Stichprobe ergibt sich aus der folgenden Formel:

N = Gesamtmenge (z. B.: 100.000)
σ = Standardabweichung (z. B.: 0,5)
e = Fehlermarge (z. B.: 0,1)
Z = Z-Wert (z. B.: 1,96)
In diesem Beispiel beträgt die Mindestgröße der Stichprobe 96,04/1,0009604 = 95,9475
Software für das Qualitätsmanagement
Ein eingeführtes Qualitätsmanagement folgt standardisierten Prozessen. Die Digitalisierung dieser standardisierten Prozesse ermöglicht sowohl eine Integration des Qualitätsmanagements in die IT-Infrastruktur als auch eine Automatisierung der Abläufe. Dadurch kann die Fehleranfälligkeit der Prozesse gesenkt werden.
Außerdem lassen sich digitalisierte Prozesse besser verfolgen und nachvollziehen. Mitarbeiter werden in der Planung, Durchführung und Überwachung von Qualitätsmaßnahmen unterstützt. Und alle Vorgabe- und Nachweisdokumente können revisionssicher gelenkt und verwaltet werden. Das Dokumentenmanagement wird dadurch vereinfacht, und der Administrationsaufwand verringert sich.
Die notwendigen technologischen Möglichkeiten zur Digitalisierung von Qualitätsmanagementprozessen stehen zur Verfügung. Damit das digitale Qualitätsmanagement funktioniert und im Unternehmen Akzeptanz findet, sind einige Dinge zu beachten: Das digitale Qualitätsmanagement muss vollständig in die IT-Infrastruktur im Unternehmen integriert sein. Insbesondere muss der Zugriff auf Daten aus dem ERP-System und aus der Fertigungsplanung gegeben sein. Außerdem müssen relevante Informationen unabhängig von den verwendeten Endgeräten in das digitale Qualitätsmanagement eingebunden werden. Nichts ist schlimmer als Systembrüche und unvollständige bzw. inkonsistente Daten. Audits sollten im digitalen Qualitätsmanagement ebenso ausgeführt werden, wie das Management von Maßnahmen, inklusive Schulungen, und das Risikomanagement. Auch das Vertragsmanagement kann ein sinnvoller Teil des digitalen Qualitätsmanagements sein. Möglichst werden die Prozesse nicht nur im digitalen Qualitätsmanagement gestaltet und geschliffen, sondern direkt aus der Anwendung heraus ausgeführt. So können Abweichungen der gelebten Praxis von den vereinbarten Vorgaben vermieden werden. Idealerweise wird durch die Anwendung auch die Qualität der Zusammenarbeit im Unternehmen gefördert.
Es gibt einige Anbieter digitaler Anwendungen für das Qualitätsmanagement. Achten Sie darauf, dass die Anwendungen plattformunabhängig eingesetzt werden können und die Prozesse an die Verhältnisse in Ihrem Unternehmen angepasst werden können. (Intrexx ist einer von diesen Anbietern.)